import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pandas_datareader as pdr
import yfinance as yfHerron Topic 4 - Portfolio Optimization
FINA 6333 for Spring 2024
This notebook covers portfolio optimization. I have not found a perfect reference that combines portfolio optimization and Python, but here are two references that I find useful:
- Ivo Welch discusses the mathematics and finance of portfolio optimization in Chapter 12 of his draft textbook on investments.
- Eryk Lewinson provides Python code for portfolio optimization in chapter 7 of his Python for Finance Cookbook, but he uses several packages that are either non-free or abandoned.
In this notebook, we will:
- Review the \(\frac{1}{n}\) portfolio (or equal-weighted portfolio) from Herron Topic 1
- Use SciPy’s
minimize()function to:- Find the minimum variance portfolio
- Find the (mean-variance) efficient frontier
In the practice notebook, we will use SciPy’s minimize() function to achieve any objective.
%precision 4
pd.options.display.float_format = '{:.4f}'.format
%config InlineBackend.figure_format = 'retina'1 The \(\frac{1}{n}\) Portfolio
We first saw the \(\frac{1}{n}\) portfolio (or equal-weighted portfolio) in Herron Topic 1. In the \(\frac{1}{n}\) portfolio, each of \(n\) assets receives an equal portfolio weight \(w_i = \frac{1}{n}\). While the \(\frac{1}{n}\) strategy seems too simple to be useful, DeMiguel, Garlappi, and Uppal (2007) show that it is difficult to beat \(\frac{1}{n}\) strategy, even with more advanced strategies.
tickers = 'MSFT AAPL TSLA AMZN NVDA GOOG'
matana = (
yf.download(tickers=tickers)
.rename_axis(columns=['Variable', 'Ticker'])
)
matana.tail()[*********************100%%**********************] 6 of 6 completed| Variable | Adj Close | Close | ... | Open | Volume | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ticker | AAPL | AMZN | GOOG | MSFT | NVDA | TSLA | AAPL | AMZN | GOOG | MSFT | ... | GOOG | MSFT | NVDA | TSLA | AAPL | AMZN | GOOG | MSFT | NVDA | TSLA |
| Date | |||||||||||||||||||||
| 2024-03-28 | 171.4800 | 180.3800 | 152.2600 | 420.7200 | 903.5600 | 175.7900 | 171.4800 | 180.3800 | 152.2600 | 420.7200 | ... | 152.0000 | 420.9600 | 900.0000 | 177.4500 | 65672700 | 38051600.0000 | 21105600.0000 | 21871200.0000 | 43521200.0000 | 77654800.0000 |
| 2024-04-01 | 170.0300 | 180.9700 | 156.5000 | 424.5700 | 903.6300 | 175.2200 | 170.0300 | 180.9700 | 156.5000 | 424.5700 | ... | 151.8300 | 423.9500 | 902.9900 | 176.1700 | 46240500 | 29174500.0000 | 24469800.0000 | 16316000.0000 | 45244100.0000 | 81562100.0000 |
| 2024-04-02 | 168.8400 | 180.6900 | 155.8700 | 421.4400 | 894.5200 | 166.6300 | 168.8400 | 180.6900 | 155.8700 | 421.4400 | ... | 154.7500 | 420.1100 | 884.4800 | 164.7500 | 49329500 | 32611500.0000 | 17598100.0000 | 17912000.0000 | 43306400.0000 | 116650600.0000 |
| 2024-04-03 | 169.6500 | 182.4100 | 156.3700 | 420.4500 | 889.6400 | 168.3800 | 169.6500 | 182.4100 | 156.3700 | 420.4500 | ... | 154.9200 | 419.7300 | 884.8400 | 164.0200 | 47602100 | 30959800.0000 | 17218400.0000 | 16475600.0000 | 36845000.0000 | 82578000.0000 |
| 2024-04-04 | 168.8200 | 180.0000 | 151.9400 | 417.8800 | 859.0500 | 171.1100 | 168.8200 | 180.0000 | 151.9400 | 417.8800 | ... | 155.0800 | 424.9900 | 904.0600 | 170.0700 | 53582300 | 41543000.0000 | 24114800.0000 | 19330000.0000 | 43300900.0000 | 122832800.0000 |
5 rows × 36 columns
returns = (
matana['Adj Close']
.iloc[:-1]
.pct_change()
.iloc[(-3 * 252):]
)
returns.describe()| Ticker | AAPL | AMZN | GOOG | MSFT | NVDA | TSLA |
|---|---|---|---|---|---|---|
| count | 756.0000 | 756.0000 | 756.0000 | 756.0000 | 756.0000 | 756.0000 |
| mean | 0.0006 | 0.0005 | 0.0007 | 0.0009 | 0.0031 | 0.0003 |
| std | 0.0169 | 0.0235 | 0.0198 | 0.0173 | 0.0335 | 0.0356 |
| min | -0.0587 | -0.1405 | -0.0963 | -0.0772 | -0.0947 | -0.1224 |
| 25% | -0.0085 | -0.0123 | -0.0097 | -0.0081 | -0.0161 | -0.0194 |
| 50% | 0.0006 | 0.0003 | 0.0010 | 0.0003 | 0.0030 | 0.0014 |
| 75% | 0.0102 | 0.0129 | 0.0110 | 0.0110 | 0.0211 | 0.0190 |
| max | 0.0890 | 0.1354 | 0.0775 | 0.0823 | 0.2437 | 0.1353 |
Before we revisit the advanced techniques from Herron Topic 1, we can calculate \(\frac{1}{n}\) portfolio returns manually, where \(r_P = \frac{\sum_{i}^{n} r_i}{n}\) Since our weights are constant (i.e., do not change over time), we rebalance our portfolio every return period. If we have daily data, rebalance daily. If we have monthly data, we rebalance monthly, and so on.
n = returns.shape[1]
p1 = returns.sum(axis=1).div(n)
p1.describe()count 756.0000
mean 0.0010
std 0.0195
min -0.0632
25% -0.0101
50% 0.0014
75% 0.0121
max 0.0980
dtype: float64Recall from Herron Topic 1 we have two better options:
- The
.mean(axis=1)method for the \(\frac{1}{n}\) portfolio - The
.dot(weights)method whereweightsis a pandas series or NumPy array of portfolio weights, allowing different weights for each asset
p2 = returns.mean(axis=1)
p2.describe()count 756.0000
mean 0.0010
std 0.0195
min -0.0632
25% -0.0101
50% 0.0014
75% 0.0121
max 0.0980
dtype: float64weights = np.ones(n) / n
weightsarray([0.1667, 0.1667, 0.1667, 0.1667, 0.1667, 0.1667])p3 = returns.dot(weights)
p3.describe()count 756.0000
mean 0.0010
std 0.0195
min -0.0632
25% -0.0101
50% 0.0014
75% 0.0121
max 0.0980
dtype: float64The .describe() method provides summary statistics for data, letting us make quick comparisons. However, we should use np.allclose() if we want to be sure that p1, p2, and p3 are similar.
np.allclose(p1, p2)Truenp.allclose(p1, p3)TrueHere is a simple example to help understand the .dot() method.
silly_n = 3
silly_r = pd.DataFrame(np.arange(2*silly_n).reshape(2, silly_n))
silly_w = np.ones(3) / 3print(
f'silly_n:\n{silly_n}',
f'silly_r:\n{silly_r}',
f'silly_w:\n{silly_w}',
sep='\n\n'
)silly_n:
3
silly_r:
0 1 2
0 0 1 2
1 3 4 5
silly_w:
[0.3333 0.3333 0.3333]silly_r.dot(silly_w)0 1.0000
1 4.0000
dtype: float64Under the hood, Python and the .dot() method (effectively) do the following calculation:
for i, row in silly_r.iterrows():
print(
f'Row {i}: ',
' + '.join([f'{w:0.2f} * {y}' for w, y in zip(silly_w, row)]),
' = ',
f'{silly_r.dot(silly_w).iloc[i]:0.2f}'
)Row 0: 0.33 * 0 + 0.33 * 1 + 0.33 * 2 = 1.00
Row 1: 0.33 * 3 + 0.33 * 4 + 0.33 * 5 = 4.002 SciPy’s minimize() Function
2.1 A Crash Course in SciPy’s minimize() Function
The minimize() function from SciPy’s optimize module finds the input array x that minimizes the output of the function fun. The minimize() function uses optimization techniques that are outside this course, but you can consider these optimization techniques to be sophisticated trial and error.
Here are the most common arguments we will pass to the minimize() function:
- We pass our first guess for input array
xto argumentx0=. - We pass additional arguments for function
funas a tuple to argumentargs=. - We pass lower and upper bounds on
xas a tuple of tuples to argumentbounds=. - We constrain our results with a tuple of dictionaries of functions to argument
contraints=.
Here is a simple example that minimizes the function quadratic() that accepts arguments x and a and returns \(y = (x - a)^2\).
import scipy.optimize as scodef quadratic(x, a=5):
return (x - a) ** 2quadratic(x=5, a=5)0quadratic(x=10, a=5)25It is helpful to plot \(y = (x - a)\) first.
x = np.linspace(-5, 15, 101)
y = quadratic(x=x)
plt.plot(x, y)
plt.xlabel(r'$x$')
plt.ylabel(r'$y$')
plt.title(r'$y = (x - 5)^2$')
plt.show()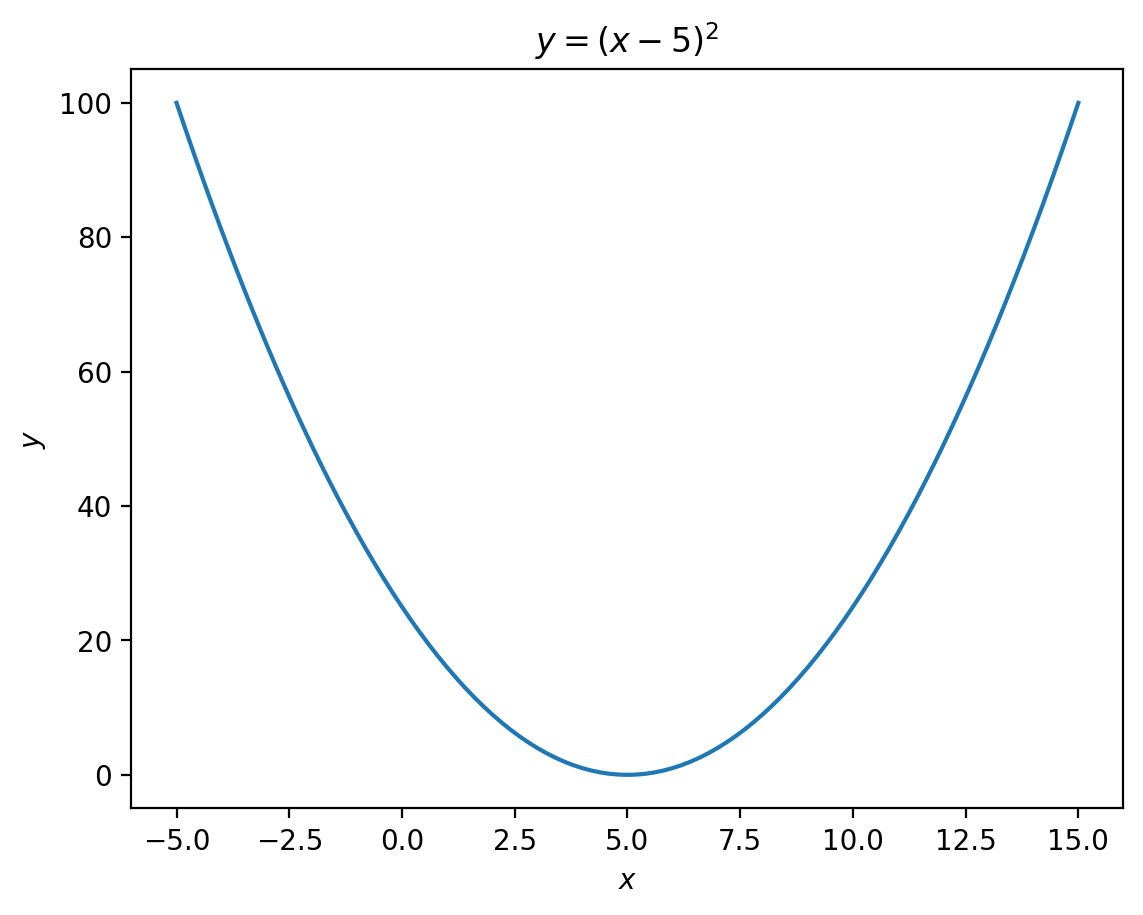
The minimum output of quadratic() occurs at \(x=5\) if we do not use bounds or constraints, even if we start far away from \(x=5\).
sco.minimize(
fun=quadratic,
x0=np.array([2001])
) message: Optimization terminated successfully.
success: True
status: 0
fun: 2.0392713450495178e-16
x: [ 5.000e+00]
nit: 4
jac: [-1.366e-08]
hess_inv: [[ 5.000e-01]]
nfev: 18
njev: 9The minimum output of quadratic() occurs at \(x=6\) if we bound x between 6 and 10 (i.e., \(6 \leq x \leq 10\)).
sco.minimize(
fun=quadratic,
x0=np.array([2001]),
bounds=((6, 10),)
) message: CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL
success: True
status: 0
fun: 1.0
x: [ 6.000e+00]
nit: 1
jac: [ 2.000e+00]
nfev: 4
njev: 2
hess_inv: <1x1 LbfgsInvHessProduct with dtype=float64>The minimum output of quadratic() occurs at \(x=6\), again, if we constrain x - 6 to be non-negative. We use bounds to limit the search space directly, and we use constraints to limit the search space indirectly based on a formula.
sco.minimize(
fun=quadratic,
x0=np.array([2001]),
constraints=({'type': 'ineq', 'fun': lambda x: x - 6})
) message: Optimization terminated successfully
success: True
status: 0
fun: 1.0000000000000018
x: [ 6.000e+00]
nit: 3
jac: [ 2.000e+00]
nfev: 6
njev: 3We can use the args= argument to pass additional arguments to fun. For example, we change the a= argument in quadratic() from the default of a=5 to a=20 with args=(20,). Note that args= expects a tuple, so we need a trailing comma , if we have one argument.
sco.minimize(
fun=quadratic,
args=(20,),
x0=np.array([2001]),
) message: Optimization terminated successfully.
success: True
status: 0
fun: 7.090392030754976e-17
x: [ 2.000e+01]
nit: 4
jac: [-1.940e-09]
hess_inv: [[ 5.000e-01]]
nfev: 18
njev: 92.2 The Minimum Variance Portfolio
We can find the minimum variance portfolio with minimize() function from SciPy’s optimize module. The minimize() function with vary an input array x (starting from argument x0=) to minimize the objective function fun= subject to the bounds and constraints in bounds= and constraints=. We will define a function port_vol() to calculate portfolio volatility. The first argument to port_vol() must be the input array x that the minimize() function searches over. For clarity, we will call this first argument x, but the argument’s name is not important.
def port_vol(x, r, ppy):
return np.sqrt(ppy) * r.dot(x).std()We will eventually need a mean portfolio return function, too.
def port_mean(x, r, ppy):
return ppy * r.dot(x).mean()[(0,1) for _ in returns][(0, 1), (0, 1), (0, 1), (0, 1), (0, 1), (0, 1)]res_mv = sco.minimize(
fun=port_vol, # objective function that we minimize
x0=np.ones(returns.shape[1]) / returns.shape[1], # initial portfolio weights are 1/n
args=(returns, 252), # additional arguments to our objective function
bounds=[(0,1) for _ in returns], # bounds limit the search space for each portfolio weights
constraints=(
{'type': 'eq', 'fun': lambda x: x.sum() - 1} # minimize drives "eq" constraints to zero
)
)
print(res_mv) message: Optimization terminated successfully
success: True
status: 0
fun: 0.2501306149875224
x: [ 5.064e-01 2.776e-17 9.326e-02 4.004e-01 2.082e-17
6.939e-18]
nit: 7
jac: [ 2.506e-01 2.591e-01 2.502e-01 2.496e-01 3.628e-01
2.920e-01]
nfev: 49
njev: 7What are the attributes of this minimum variance portfolio?
def print_port_res(w, r, title, ppy=252, tgt=None):
width = len(title)
rp = r.dot(w)
mu = ppy * rp.mean()
sigma = np.sqrt(ppy) * rp.std()
if tgt is not None:
er = rp.sub(tgt)
sr = np.sqrt(ppy) * er.mean() / er.std()
else:
sr = None
return print(
title,
'=' * width,
'',
'Performance',
'-' * width,
'Return:'.ljust(width - 6) + f'{mu:0.4f}',
'Volatility:'.ljust(width - 6) + f'{sigma:0.4f}',
'Sharpe Ratio:'.ljust(width - 6) + f'{sr:0.4f}\n' if sr is not None else '',
'Weights',
'-' * width,
'\n'.join([f'{_r}:'.ljust(width - 6) + f'{_w:0.4f}' for _r, _w in zip(r.columns, w)]),
sep='\n',
)print_port_res(w=res_mv['x'], r=returns, title='Minimum Variance Portfolio')Minimum Variance Portfolio
==========================
Performance
--------------------------
Return: 0.1897
Volatility: 0.2501
Weights
--------------------------
AAPL: 0.5064
AMZN: 0.0000
GOOG: 0.0933
MSFT: 0.4004
NVDA: 0.0000
TSLA: 0.00002.3 The Mean-Variance Efficient Frontier
We will use the minimize() function to map the efficient frontier. Here is a basic outline:
- Create a NumPy array
tretof target returns - Create an empty list
res_efofminimize()results - Loop over
tret, passing each as a constraint to theminimize()function - Append each
minimize()result tores_ef
returns.mean()Ticker
AAPL 0.0006
AMZN 0.0005
GOOG 0.0007
MSFT 0.0009
NVDA 0.0031
TSLA 0.0003
dtype: float64tret = 252 * np.linspace(returns.mean().min(), returns.mean().max(), 25)
tretarray([0.0675, 0.0968, 0.1262, 0.1555, 0.1849, 0.2143, 0.2436, 0.273 ,
0.3023, 0.3317, 0.3611, 0.3904, 0.4198, 0.4492, 0.4785, 0.5079,
0.5372, 0.5666, 0.596 , 0.6253, 0.6547, 0.684 , 0.7134, 0.7428,
0.7721])We will loop over these target returns, finding the minimum variance portfolio for each target return.
res_ef = []
for t in tret:
_ = sco.minimize(
fun=port_vol, # minimize portfolio volatility
x0=np.ones(returns.shape[1]) / returns.shape[1], # initial portfolio weights of 1/n
args=(returns, 252), # additional arguments to fun, in order
bounds=[(0, 1) for c in returns.columns], # bounds limit the search space for each portfolio weight
constraints=(
{'type': 'eq', 'fun': lambda x: x.sum() - 1}, # constrain sum of weights to one
{'type': 'eq', 'fun': lambda x: port_mean(x=x, r=returns, ppy=252) - t} # constrains portfolio mean return to the target return
)
)
res_ef.append(_)List res_ef contains the results of all 25 minimum-variance portfolios. For example, res_ef[0] is the minimum variance portfolio for the lowest target return.
returns.columnsIndex(['AAPL', 'AMZN', 'GOOG', 'MSFT', 'NVDA', 'TSLA'], dtype='object', name='Ticker')res_ef[0] message: Optimization terminated successfully
success: True
status: 0
fun: 0.5658612930635905
x: [ 0.000e+00 1.206e-10 0.000e+00 1.775e-16 0.000e+00
1.000e+00]
nit: 3
jac: [ 1.383e-01 1.648e-01 1.271e-01 1.179e-01 2.690e-01
5.659e-01]
nfev: 21
njev: 3I typically check that all portfolio volatility minimization succeeds. If a portfolio volatility minimization fails, we should check our function, bounds, and constraints.
for r in res_ef:
assert r['success'] We can combine the target returns and volatilities into a data frame ef.
ef = pd.DataFrame(
{
'tret': tret,
'tvol': np.array([r['fun'] if r['success'] else np.nan for r in res_ef])
}
)
ef.head()| tret | tvol | |
|---|---|---|
| 0 | 0.0675 | 0.5659 |
| 1 | 0.0968 | 0.3984 |
| 2 | 0.1262 | 0.2974 |
| 3 | 0.1555 | 0.2597 |
| 4 | 0.1849 | 0.2504 |
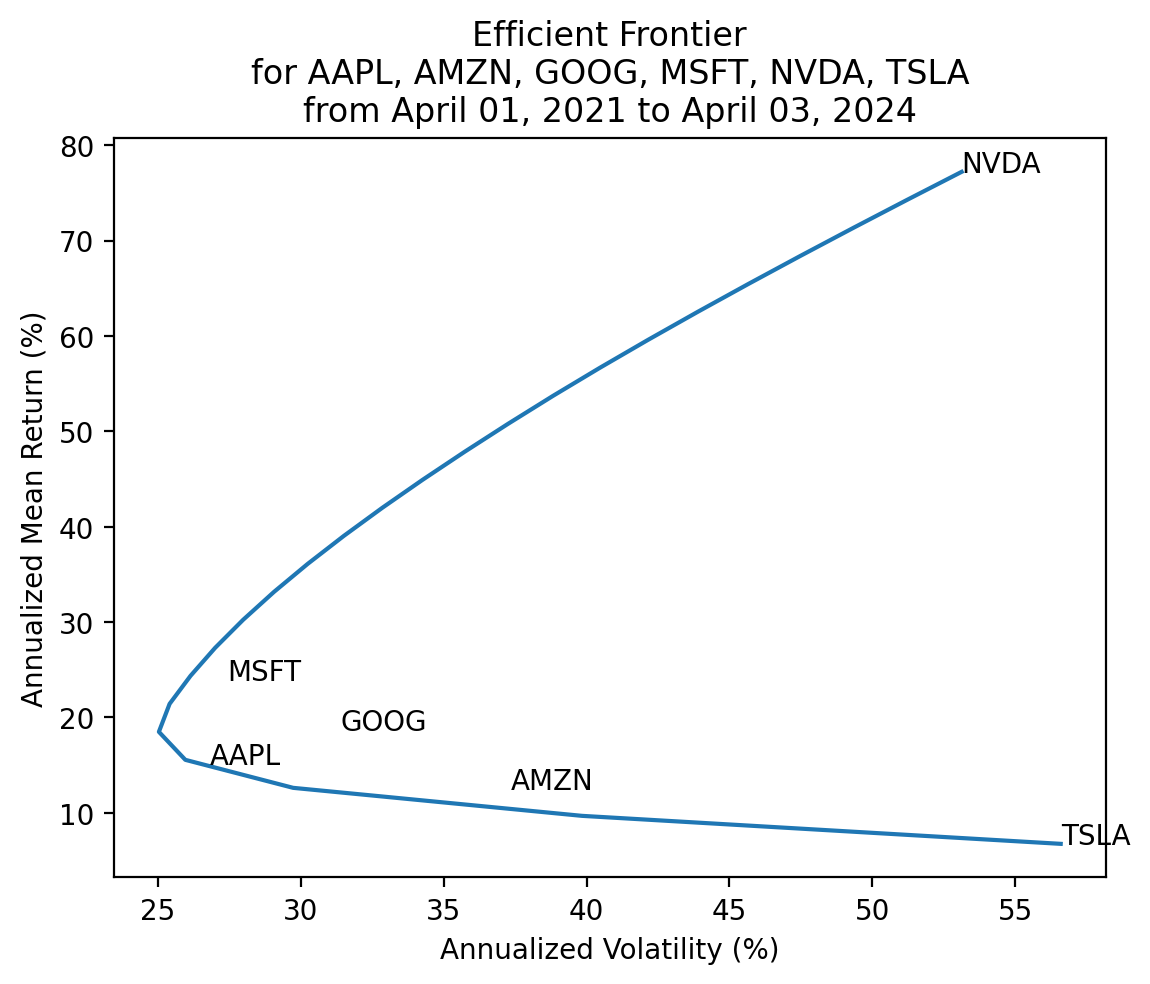
ef.mul(100).plot(x='tvol', y='tret', legend=False)
plt.ylabel('Annualized Mean Return (%)')
plt.xlabel('Annualized Volatility (%)')
plt.title(
f'Efficient Frontier' +
f'\nfor {", ".join(returns.columns)}' +
f'\nfrom {returns.index[0]:%B %d, %Y} to {returns.index[-1]:%B %d, %Y}'
)
for t, x, y in zip(
returns.columns,
returns.std().mul(100*np.sqrt(252)),
returns.mean().mul(100*252)
):
plt.annotate(text=t, xy=(x, y))
plt.show()